Intro

Normalizing flows are an interesting approach to transform simple distributions to more complex ones without sacraficing the computational benefits that make those simple distributions appealing in the context of probabilistic inference.

The idea was introduced in its popular form to the machine learning community in Rezende et al. where the authors begin their experiments with a simple test of expressivity using a series of toy densities.

I thought it would be a good practical introduction to normalizing flows to try and replicate this set of simple tests with pytorch. All the code can be found on github.

Context

The utility of normalizing flows is best understood in the context of variational inference. I’ll provide some intuition here but for a thorough treatment of variational inference I would recommend: Variational Inference: A Review for Statisticians, or Graphical Models, Exponential Families, and Variational Inference

Following Blei et al:

Consider a joint distribution $p(z, x) = p(z) p(x|z)$ with latent variables $\mathbb{z}=z_{1:m}$ and observations $\mathbb{x}=x_{1:n}$ With $z \sim p(\mathbb{z})$. Bayesian inference then relates the data and the posterior $p(z|x)$ as follows:

$p(z|x)\propto p(z)p(x|z)$

Normalizing the RHS is often intractable and so approximate inference is needed.

Variational inference achieves this by using a simpler family of distributions $\mathcal{D}$ over the latent variables and then optimizing the parameters of this simpler family (the variational parameters) to be as good as possible. The measure of “goodness” usually used is KL divergence to the true posterior:

$q^{*}(z)= argmin_{q(x)\in \mathcal{D}} KL(q(z) || p(z|x))$

Theres a lot more to be said here but the problem that normalizing flows attempts to adress is already clear: if our family is too simple, even the optimal setting of the variational parameters could make our approximate posterior quite far from the true posterior. The ability to enable more complex variational distributions without sacraficing the ability to do this optimization is what makes normalizing flows appealing.

Normalizing flows

The basic idea is to pass a sample from our original simple base distribution through a series of invertible transformations or flows. This transformed sample is a sample from the final distribution. The invertibility gives a closed form relationship between the density of the initial distribution and the final.

Consider an invertible smooth mapping $$f: \mathcal{R}^{d} \to \mathcal{R}^d$$ with an inverse $f^{-1} = g$ Given a random variable $z \sim q$ $z^{‘} = f(z)$ is distributed as:

$$q(z’) = q(z) \lvert det \frac{\partial f^{-1}}{\partial z^{‘}} \rvert) = q(z)\rvert det \frac{\partial f}{\partial z} \lvert$$

So if we have $k$ flows and transform our iniital sample $Z_k= f_K \circ … \circ f_2 \circ f_1(z_0)$

We can get the final density as follows:

$lnq_K(z_K)= ln_{q_0}(z_0)-\sum_{k=1}^K ln \lvert det \frac{\partial f_k}{\partial z_{z_{k-1}}}\rvert$

Nice!

Now all we need invertible transformations to use. The authors propose a family of transformations that look like

$f(z)=z+uh(w^T z + b)$ $w\in \mathcal{R}^D, u \in \mathcal{R}^D, b \mathcal{R}$ $h$ is an elementwise nonlinearity.

$$\psi(z) = h’(w^Tz + b)w$$ $$\rvert det \frac{\partial f}{\partial z} = \lvert 1+ u^T \psi(z) \rvert $$

These are called planar flows.

Our formula for the final log density looks like

$$ln q_K(z_K) = ln_{q_0}(z) - \sum_{k=1}^K ln \lvert 1+ u_k^T \psi_k(z_{k-1})\rvert$$

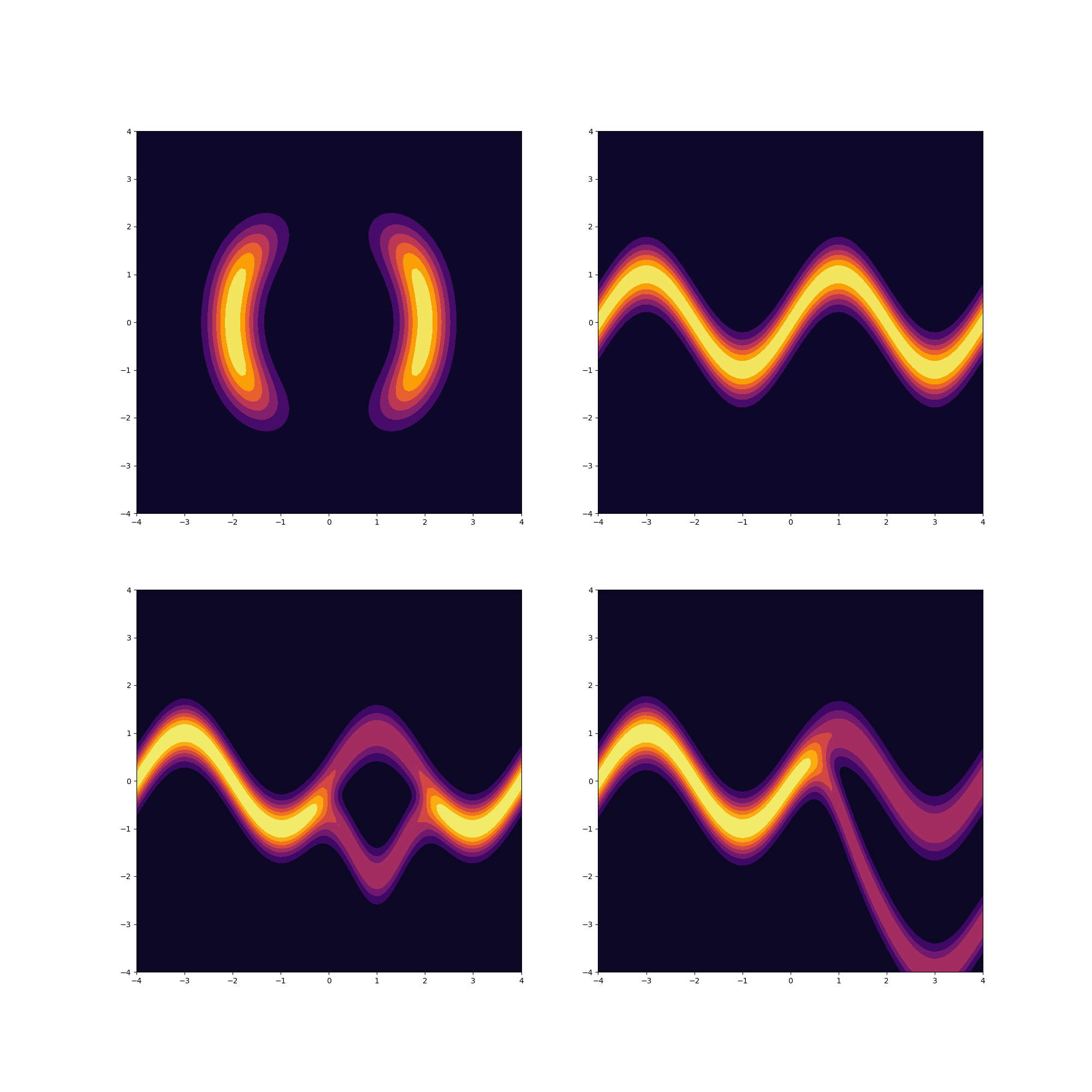
Potential functions

The paper proposes four potential functions $U(z)$ with unormalized densities $p(z) \propto exp[-U(z)]$

Our final bound to optimize is:

$F(x) = \mathbb{E}_{q_0(z_0)} [\ln{q_0(z_0)}] - \beta \mathbb{E}_{q_0(z_0)} [\log p(x, z_{K})] - \mathcal{E}_{q_0(z_0)} [\sum_{k=1}^K \ln {\lvert 1 + u^{T}_{k} \psi (z_k-1)}]$

The potential functions look as follows:

Implementation

We first implement our densities as simple functions that take a 2-D point and return a scalar value. For example, take the code for the first potential in the figure above:

def w_1(z):
    return torch.sin((2 * math.pi * z[:, 0]) / 4)


def w_2(z):
    return 3 * torch.exp(-.5 * ((z[:, 0] - 1) / .6) ** 2)


def sigma(x):
    return 1 / (1 + torch.exp(- x))


def w_3(z):
    return 3 * sigma((z[:, 0] - 1) / .3)


def pot_1(z):
    z_1, z_2 = z[:, 0], z[:, 1]
    norm = torch.sqrt(z_1 ** 2 + z_2 ** 2)
    outer_term_1 = .5 * ((norm - 2) / .4) ** 2
    inner_term_1 = torch.exp((-.5 * ((z_1 - 2) / .6) ** 2))
    inner_term_2 = torch.exp((-.5 * ((z_1 + 2) / .6) ** 2))
    outer_term_2 = torch.log(inner_term_1 + inner_term_2 + 1e-7)
    u = outer_term_1 - outer_term_2
    return - u